MATEMÁTICAS
Análisis de la segunda derivada
Aplicaciones de las derivadas
Efectivamente, cuando la función es cóncava hacia arriba (abajo) en un intervalo I sucede que la pendiente de la recta tangente crece (decrece) en la medida que se va de izquierda a derecha del intervalo I. Esto quiere decir que la derivada f0 es una función creciente
La segunda derivada ayuda a determinar los intervalos de concavidad de una función.

Una función es convexa en un intervalo de su dominio cuando:
Dados dos puntos cualesquiera de dicho intervalo y , el segmento que une los puntos y siempre queda por encima de la gráfica.

Una función es cóncava en un intervalo de su dominio cuando:
Dados dos puntos cualesquiera de dicho intervalo y , el segmento que une los puntos y siempre queda por debajo de la gráfica
Ejemplos:

Función convexa hacia arriba
Para determinar si una función es convexa hacia arriba, utilizamos el criterio de la segunda derivada. Una función f(x) es convexa hacia arriba en un intervalo si su segunda derivada f′′(x) es mayor o igual que cero en ese intervalo.
Ejemplo
Encontrar los intervalos donde la siguiente función es cóncava o convexa:

Primero notemos que el dominio de la función es D=R .
Ahora utilizaremos el criterio de concavidad-convexidad de la segunda derivada, el cual nos dice que la que función será convexa en los intervalos donde la segunda derivada sea positiva y será cóncava en los intervalos donde la segunda derivada sea negativa.
Primero procedemos a obtener la segunda derivada


Luego procedemos a obtener los puntos donde la segunda derivada se anula, lo cual nos dará los puntos de inflexión

Finalmente, analizamos en que intervalos la segunda derivada es positiva o negativa


Esto ultimo nos dice que f(x) es convexa en (-∞,0) y cóncava en (0,∞)

Otro ejemplo:
Una función f(x) es convexa hacia arriba en un intervalo si, para cualquier par de puntos x1 y x2 en ese intervalo, la siguiente condición se cumple:

Primera derivada de f(x) = x^2:
Segunda derivada: f''(x) = 2
La segunda derivada f''(x) = 2 es positiva para todos los valores de x. Cuando la segunda derivada de una función es positiva en un intervalo, esto implica que la función es convexa hacia arriba en ese intervalo.

Función cóncava hacia arriba
Función: f(x) = x^3 - 3x^2 + 4
Calcular la primera derivada: f'(x) = 3x^2 - 6x
Calcular la segunda derivada: f''(x) = 6x - 6Encontrar los puntos críticos de la segunda derivada: 6x−6=0 ⟹ x=1
Determinar el signo de la segunda derivada:

La función f(x) es cóncava hacia abajo en el intervalo (−∞,1) y cóncava hacia arriba en el intervalo (1,∞).

Función es convexa hacia abajo
Consideremos la función: f(x) = -x^2 + 4
Calculamos la primera derivada de la función:
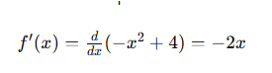
Calculamos la segunda derivada:

La función f(x) es convexa hacia abajo si su segunda derivada es menor que cero para todos los x. En este caso:
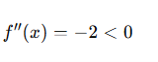
Dado que la segunda derivada es constante y negativa, concluimos que la función es convexa hacia abajo en todo su dominio.
Función cóncava hacia abajo
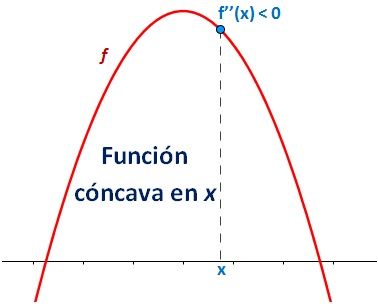
Para estudiar si una función es cóncava en un punto x, debemos recurrir a la derivada segunda de la función. Sean f y f ' derivables.
Diremos que f es cóncava en el punto x si la segunda derivada de f en x es menor que 0 (f ''(x) < 0).
Ejemplo
Sea la función cuadrática f(x) = –x2. Calculamos la segunda derivada de f, es decir f ''(x).

La segunda derivada es negativa, siendo f ''(x) = -2 < 0 en todos los puntos, por lo que la función es estrictamente cóncava en todo su dominio.